一,Maxwell Equation 簡(jiǎn)介
麥克斯韋方程是一組描述電磁學(xué)世界的4個(gè)復(fù)雜方程。這些方程描述了電場(chǎng)和磁場(chǎng)如何傳播、相互作用,以及它們?nèi)绾问艿轿矬w的影響。
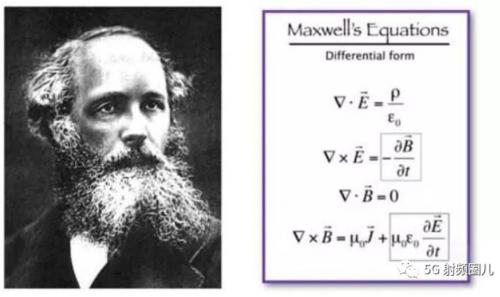
詹姆斯·克拉克·麥克斯韋(James Clerk Maxwell)[1831-1879]是愛因斯坦/牛頓級(jí)別的天才,他采用了一組已知的實(shí)驗(yàn)定律(法拉第定律、安培定律),并將它們統(tǒng)一成一組對(duì)稱的相干方程,稱為麥克斯韋方程。麥克斯韋是最早確定電磁波傳播速度與光速相同的人之一,因此得出結(jié)論:電磁波和可見光實(shí)際上是同一回事。
麥克斯韋方程是理解天線和電磁學(xué)的關(guān)鍵。它們看起來非常復(fù)雜,以至于大多數(shù)電子工程師和物理學(xué)家都不知道它們的真正含義。被復(fù)雜的數(shù)學(xué)所籠罩(人們?cè)谟懻撨@些問題時(shí)可能會(huì)覺得自己很聰明),很難真正理解這些方程。

如果可能的話,我將避免出現(xiàn)數(shù)學(xué)困難,而是描述方程的含義。別害怕,數(shù)學(xué)太復(fù)雜了,那些真正理解復(fù)雜向量演算的人,除了最簡(jiǎn)單的情況外,仍然無法應(yīng)用麥克斯韋方程。因此,麥克斯韋方程的直觀知識(shí)遠(yuǎn)遠(yuǎn)優(yōu)于基于數(shù)學(xué)操作的知識(shí)。要了解這個(gè)世界,你必須了解方程的含義,而不僅僅是了解數(shù)學(xué)結(jié)構(gòu)。我相信教授電磁學(xué)和麥克斯韋方程的公認(rèn)方法不能產(chǎn)生理解。接下來,我們來談?wù)勥@些方程。
麥克斯韋方程是定律,就像重力定律一樣。這些方程是宇宙用來控制電場(chǎng)和磁場(chǎng)行為的規(guī)則。電流的流動(dòng)會(huì)產(chǎn)生磁場(chǎng)。如果電流隨時(shí)間變化(如在任何波或周期信號(hào)中),磁場(chǎng)也會(huì)產(chǎn)生電場(chǎng)。麥克斯韋方程表明,分離電荷(正電荷和負(fù)電荷)會(huì)產(chǎn)生一個(gè)電場(chǎng)——如果這個(gè)電場(chǎng)在時(shí)間上發(fā)生變化,也會(huì)產(chǎn)生一個(gè)傳播電場(chǎng),進(jìn)而產(chǎn)生一個(gè)支撐磁場(chǎng)。
要比大多數(shù)工程學(xué)或物理學(xué)博士更直觀地理解麥克斯韋方程,請(qǐng)點(diǎn)擊上面的鏈接和定義。你會(huì)發(fā)現(xiàn)復(fù)雜的數(shù)學(xué)掩蓋了這些方程內(nèi)在的優(yōu)雅——你會(huì)了解宇宙是如何操作電磁機(jī)器的。
二,Maxwell Equation 的數(shù)學(xué)基礎(chǔ)
這個(gè)散度算子就是上圖 麥克斯韋方程組中的那個(gè)倒三角和點(diǎn)組成的符號(hào)
文章盡可能的不用數(shù)學(xué)方法去描述這個(gè)散度算子:
首先散度的定義即是:點(diǎn)(x,y,z)處的散度是該點(diǎn)周圍曲面的矢量流的度量。也就是說,假設(shè)一個(gè)向量場(chǎng)代表水流。如果散度是一個(gè)正數(shù),這意味著水從這個(gè)點(diǎn)流出(就像一個(gè)水嘴-這個(gè)位置被認(rèn)為是一個(gè)源頭)。如果散度是一個(gè)負(fù)數(shù),那么水就流入這個(gè)點(diǎn)(就像一個(gè)排水溝-這個(gè)位置被稱為水槽)。
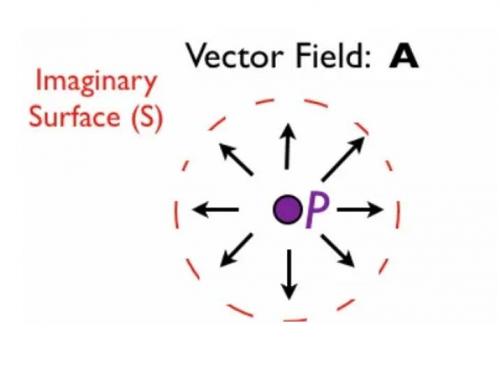
我將舉一些例子來說明這一點(diǎn)。首先,假設(shè)我們有一個(gè)向量場(chǎng)(由向量函數(shù)a給出),如圖1所示,我們想知道P點(diǎn)的散度是多少:
我們還畫了一個(gè)圍繞點(diǎn)P的假想表面。現(xiàn)在想象向量A代表水流。那么,如果你把從地表流出的水量加起來,這個(gè)量會(huì)是正數(shù)嗎?答案是肯定的:水在S表面的每個(gè)位置都從表面流出。因此,我們可以說P的散度是正的。
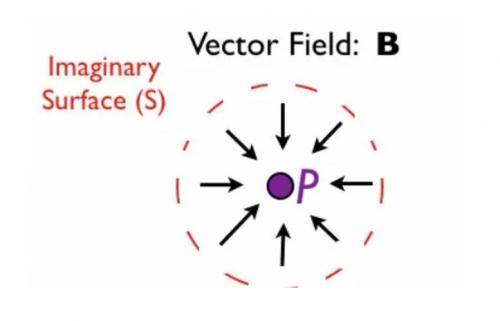
再舉一個(gè)簡(jiǎn)單的例子,如圖2所示。我們?cè)邳c(diǎn)P周圍有一個(gè)新的向量場(chǎng)B:
在圖2中,如果我們想象水的流動(dòng),我們會(huì)看到P點(diǎn)像一個(gè)排水溝或水槽。在這種情況下,流出表面的氣流是負(fù)的,因此,P處的場(chǎng)B的散度是負(fù)的。
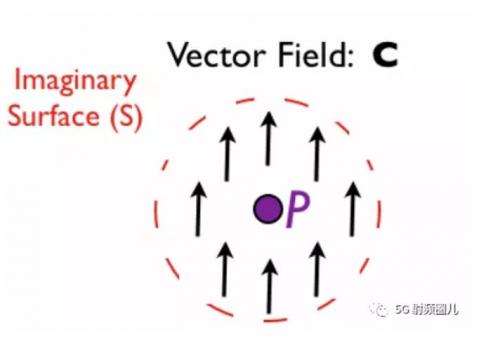
很簡(jiǎn)單,嗯?這里還有幾個(gè)例子。圖3在點(diǎn)周圍有一個(gè)向量場(chǎng)C:
在圖3中,如果C表示水的流量,那么更多的水是流入還是流出地表?在圖3的頂部,水從表面流出,但在底部流入。由于場(chǎng)進(jìn)出表面的流量相等,散度為零。
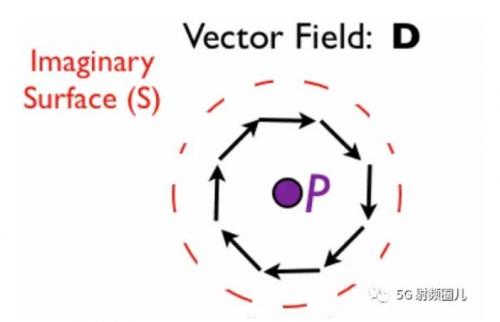
鑒于您可能玩得很開心,讓我們?cè)倥e兩個(gè)例子。查看圖4:
在圖4中,我們有一個(gè)繞著點(diǎn)P的向量場(chǎng)D。流是正的(流出表面)還是負(fù)的(流入表面)?在沿曲面S的每個(gè)點(diǎn)處,場(chǎng)沿曲面切向流動(dòng)。因此,場(chǎng)不是在每個(gè)點(diǎn)流入或流出表面。因此,在P處,我們得到D的散度等于0。
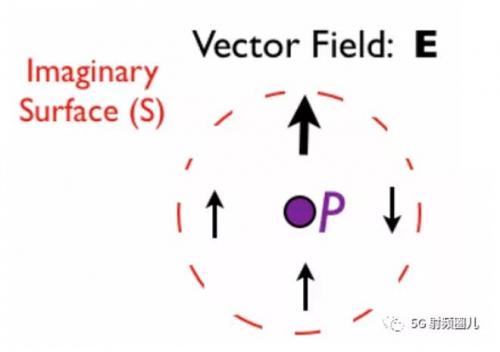
讓我們看最后一個(gè)例子,圖5中的字段E:
向量場(chǎng)E在P點(diǎn)上方有一個(gè)大向量,表示那里有一個(gè)很強(qiáng)的場(chǎng),很多水從表面流出。P左邊的向量很小,與曲面相切,因此在該點(diǎn)沒有流入或流出S的流。P右邊的向量也是如此,P下面的向量很小,表示流入地表的水量較小。因此,我們可以猜測(cè)散度是正的-流出地表的水比流入地表的水多。
當(dāng)然如果你的數(shù)學(xué)比較好的話,請(qǐng)點(diǎn)擊閱讀原文查看散度的數(shù)學(xué)定義。小木匠比較懶,不再對(duì)數(shù)學(xué)定義做更多學(xué)習(xí)。
2.2 旋度和旋度算子
這個(gè)旋度算子就是麥克斯韋方程組中式3和式4用到的那個(gè)倒三角和x的組合:
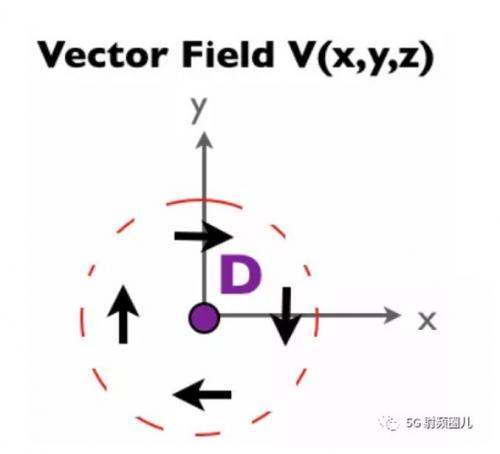
旋度是向量場(chǎng)旋轉(zhuǎn)的量度。為了理解這一點(diǎn),我們將再次使用流動(dòng)水的類比來表示向量函數(shù)(或向量場(chǎng))。在圖1中,我們有一個(gè)向量函數(shù)(V),我們想知道場(chǎng)是否在D點(diǎn)旋轉(zhuǎn)(也就是說,我們想知道旋度是否為零)。
若要確定場(chǎng)是否旋轉(zhuǎn),請(qǐng)假設(shè)D點(diǎn)處有一個(gè)水輪。如果表示水流的矢量場(chǎng)會(huì)旋轉(zhuǎn)水輪,則旋度不為零:
在上圖中,我們可以看到水輪將順時(shí)針旋轉(zhuǎn)。因此,這個(gè)向量場(chǎng)在點(diǎn)D處有一個(gè)旋度。
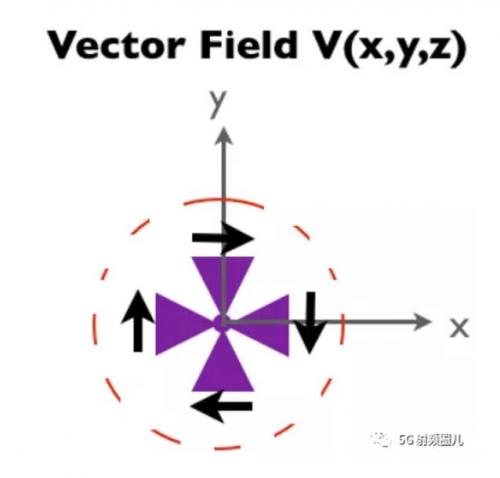
我們現(xiàn)在必須使事情更復(fù)雜。圖2的旋度是正的還是負(fù)的,方向是什么?因?yàn)槲覀冇^察的是在x-y平面上旋轉(zhuǎn)水車的旋度,所以旋度的方向被認(rèn)為是z軸(垂直于水車的平面)。此外,卷曲遵循右手法則:如果你的拇指指向+z方向,那么你的右手將沿著正卷曲的方向繞軸卷曲。對(duì)于圖2,如果水輪以逆時(shí)針方向旋轉(zhuǎn),則旋度為正。如果水車順時(shí)針旋轉(zhuǎn),旋度將為負(fù)值。
在上圖中,水輪順時(shí)針旋轉(zhuǎn)。因此,圖1中向量場(chǎng)旋度的z分量為負(fù)。
你可以想象,旋度也有x和y分量。因此,旋度作用于向量場(chǎng),結(jié)果是三維向量。也就是說,如果我們知道一個(gè)向量場(chǎng),我們就可以計(jì)算任意點(diǎn)的旋度,結(jié)果就是一個(gè)向量(表示x、y和z方向)。
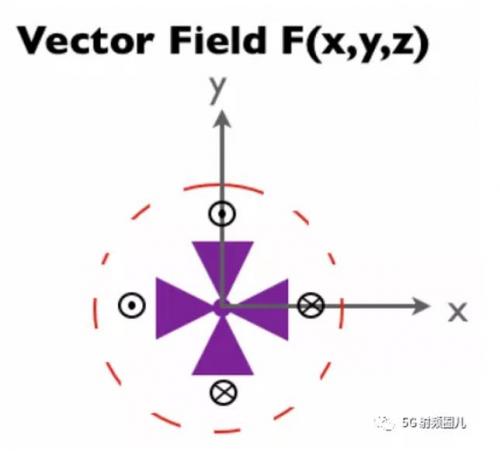
再舉一個(gè)新的例子。假設(shè)圖3中的向量場(chǎng)F具有z向場(chǎng)。讓 符號(hào)表示+z方向的向量,
符號(hào)表示+z方向的向量, 符號(hào)表示-z方向的向量:
符號(hào)表示-z方向的向量:
如果水在輪子周圍上下流動(dòng),輪子會(huì)旋轉(zhuǎn)嗎?答案是否定的。當(dāng)輪子在x-y平面上時(shí),只有x和y方向的向量可以使輪子旋轉(zhuǎn)。因此,可以忽略z向向量場(chǎng)來確定旋度的z分量。
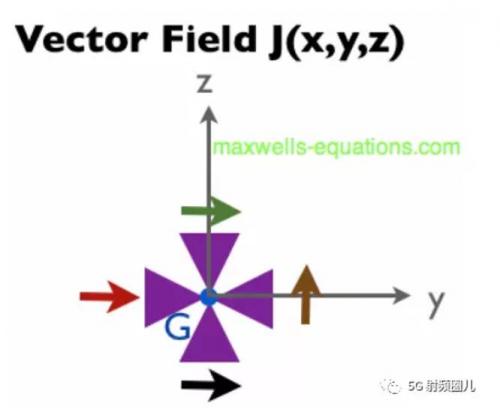
現(xiàn)在,讓我們舉更多的例子來確保我們理解旋度。關(guān)于下圖中G點(diǎn)處向量場(chǎng)J的旋度,我們能說些什么?
圖4中的旋度是正、負(fù)還是零?它朝什么方向?首先,由于水車在y-z平面上,旋度的方向(如果不是零)將沿x軸。現(xiàn)在,我們想知道旋度是正的(逆時(shí)針旋轉(zhuǎn))還是負(fù)的(順時(shí)針旋轉(zhuǎn))。
上圖中的紅色向量在+y方向。但是,它不會(huì)旋轉(zhuǎn)水輪,因?yàn)樗苯又赶蛩喌闹行模粫?huì)產(chǎn)生旋轉(zhuǎn)。圖4中的綠色向量將嘗試沿順時(shí)針方向旋轉(zhuǎn)水輪機(jī),而黑色向量將嘗試沿逆時(shí)針方向旋轉(zhuǎn)水輪機(jī),因此綠色向量和黑色向量抵消,不產(chǎn)生旋轉(zhuǎn)。但是,棕色矢量將逆時(shí)針方向旋轉(zhuǎn)水輪。因此,圖4中所有矢量的凈效應(yīng)是逆時(shí)針旋轉(zhuǎn)。結(jié)果是圖4中的旋度是正的,并且在+x方向上。
一般來說,向量場(chǎng)有[x,y,z]個(gè)分量。得到的旋度也是一個(gè)包含[x,y,z]分量的向量。用水車在三個(gè)方向上畫三維場(chǎng)是很困難的,但是如果你理解上面的例子,你可以把上面的二維思想推廣到三維。現(xiàn)在我們將給出旋度的完整數(shù)學(xué)定義。
下面公式式麥克斯韋方程組的微分形式,詳細(xì)介紹在長尾的文章內(nèi)有。我們這邊先以小木匠學(xué)習(xí)的這篇英文文檔說起。
高斯定律是麥克斯韋方程的第一個(gè),它決定了電場(chǎng)在電荷周圍的行為。高斯定律可以用電通量密度和電荷密度寫成:
這個(gè)就用到了散度算子,大家還不理解的話還可以回到上文再學(xué)習(xí)。
小木匠提示一下:散度就是點(diǎn)(x,y,z)處的散度是該點(diǎn)周圍曲面的矢量流的度量。
方程[1]以點(diǎn)的形式稱為高斯定律。也就是說,方程[1]在空間的任何一點(diǎn)都是正確的。也就是說,如果某個(gè)地方存在電荷,那么該點(diǎn)的D的散度是非零的,否則等于零。
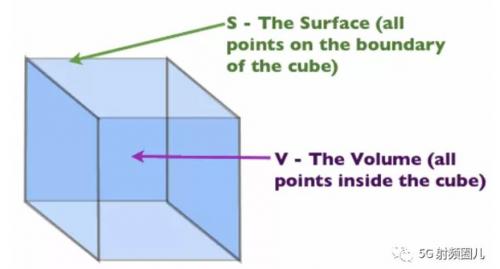
為了更直觀地了解高斯定律,讓我們看一下積分形式的高斯定律。為此,我們假設(shè)某個(gè)任意卷(我們稱之為V)有一個(gè)邊界(寫為S)。然后在體積V上積分方程[1]得到積分形式的高斯定律:
我可能說得不太清楚,但讓我們很快來看看。以圖1為例。我們有一個(gè)體積V,就是立方體。曲面S是立方體的邊界(即構(gòu)成體積邊界的6個(gè)平面)。
方程[2]指出,體積V(=封閉電荷)內(nèi)的電荷量等于從表面S流出的總磁通量(D)。也就是說,要確定離開區(qū)域V的磁通量,我們只需要知道體積內(nèi)有多少電荷。我們用方程[3]中定義的更多項(xiàng)重寫方程[2]:

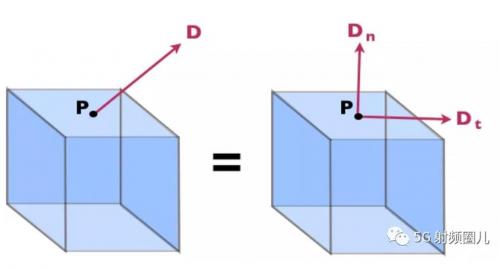
上圖中的立方體示例可能有助于說明這一點(diǎn)。看看圖2中的P點(diǎn),我們已經(jīng)畫出了D場(chǎng)向量:
我們可以根據(jù)切向分量和法向分量重寫任何字段,如圖2所示。從方程[3]中,我們只對(duì)D法向(正交或垂直)到曲面S的分量感興趣,我們把它寫成Dn。切向分量Dt沿表面流動(dòng)。如果你把D場(chǎng)想象成水的流動(dòng),那么只有成分Dn會(huì)對(duì)水有貢獻(xiàn),實(shí)際上離開體積Dt只是水繞著表面流動(dòng)。
因此,高斯定律是一個(gè)數(shù)學(xué)陳述,即任何體積的總電流等于內(nèi)部的總電荷。因此,如果所討論的體積內(nèi)沒有電荷,則流出該區(qū)域的凈電流為零。如果在一個(gè)體積內(nèi)有正電荷,那么在電荷周圍的任何體積中都存在正數(shù)量的電流。如果一個(gè)體積內(nèi)有負(fù)電荷,則存在一個(gè)負(fù)數(shù)量的電通量(即電通量進(jìn)入該體積)。
這有什么關(guān)系?高斯定律指出電荷是電場(chǎng)的源或匯。
如果你再次使用水的類比,正電荷會(huì)導(dǎo)致一個(gè)體積的水流出,這意味著正電荷就像一個(gè)水源(一個(gè)水龍頭——把水抽到一個(gè)區(qū)域)。相反,負(fù)電荷會(huì)導(dǎo)致流入一個(gè)體積——這意味著負(fù)電荷就像一個(gè)水槽(磁場(chǎng)流入一個(gè)區(qū)域并在電荷上終止)。
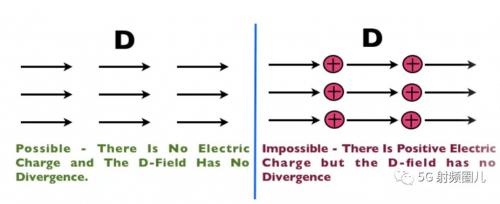
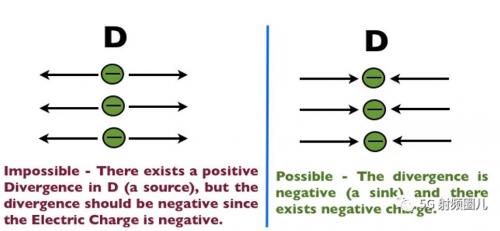
這給了我們很多關(guān)于場(chǎng)在任何場(chǎng)景中的物理行為的直覺。例如,對(duì)于電場(chǎng),這里有可能也有不可能的情況,這是由宇宙在高斯定律中決定的:
如果你觀察到D場(chǎng)在電荷周圍的行為方式,你可能會(huì)注意到高斯定律相當(dāng)于電荷的力方程,這就產(chǎn)生了點(diǎn)電荷的E場(chǎng)方程:
方程[4]表明電荷對(duì)它們施加力,這意味著存在著遠(yuǎn)離正電荷和朝向負(fù)電荷的電場(chǎng)。這意味著反電荷吸引負(fù)電荷排斥。由于D和E與介電常數(shù)有關(guān),我們發(fā)現(xiàn)高斯定律是電荷力方程的一個(gè)更為形式化的表述。
總之,高斯定律意味著以下情況是正確的:
D和E場(chǎng)線向負(fù)電荷方向發(fā)散
D場(chǎng)在空間任意區(qū)域(體積)上的發(fā)散量,正好等于該區(qū)域中的電荷凈額。
不得不佩服高斯的niubility,麥克斯韋方程組,高斯提供了兩個(gè)重要公式。
你可以看到這兩個(gè)方程都指定了所討論的場(chǎng)的散度。對(duì)于top方程,我們知道電場(chǎng)的高斯定律表明,磁通密度D的散度等于體積電荷密度。而第二個(gè)方程,高斯磁定律表明磁通密度(B)的散度為零。
嗯-是的。但碰巧沒有人發(fā)現(xiàn)過磁電荷,不是在實(shí)驗(yàn)室里,街上或地鐵里。因此,在找到這個(gè)假設(shè)的磁荷之前,我們將磁場(chǎng)的高斯定律的右邊設(shè)為零:
由于B和磁場(chǎng)H與磁導(dǎo)率有關(guān),我們?cè)诜匠蘙2]中注意到磁場(chǎng)的散度也是零。
現(xiàn)在,你小時(shí)候可能玩過磁鐵,這些磁性物體吸引了其他磁鐵,就像電荷排斥或吸引電荷一樣。然而,這些磁鐵有一些特別之處——它們總是有一個(gè)積極和消極的結(jié)局。這意味著每個(gè)磁性物體都是一個(gè)磁偶極子,有一個(gè)南北極。不管你把磁場(chǎng)分成兩半多少次,它只會(huì)形成更多的磁偶極子。高斯磁定律指出磁單極子不存在,或者至少我們還沒有找到它們。
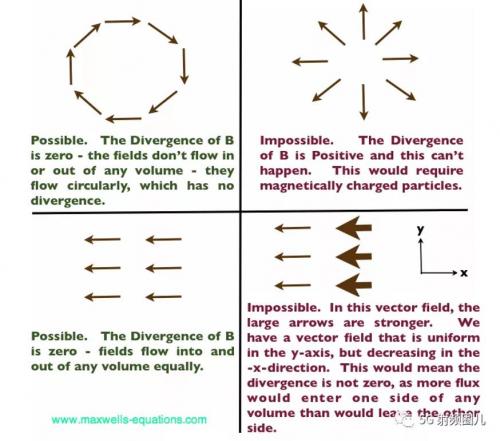
因?yàn)槲覀冎来磐芏鹊纳⒍瓤偸橇悖晕覀儸F(xiàn)在對(duì)這些磁場(chǎng)的行為有了一點(diǎn)了解。我將舉幾個(gè)合法和非法磁場(chǎng)的例子,這是高斯定律對(duì)磁場(chǎng)的結(jié)果:
總之,麥克斯韋方程組的第二個(gè)——高斯磁性定律——意味著:
在任何體積中,B或H場(chǎng)的散度總是為零
離開磁偶極子,磁場(chǎng)在一個(gè)閉環(huán)中流動(dòng)。這是真的,即使是平面波,恰好有一個(gè)無限半徑的環(huán)。
這就是磁場(chǎng)的高斯定律。如果你理解高斯電場(chǎng)定律,這不是很復(fù)雜。
終于輪到天才法拉第出場(chǎng)了,目前比較火的號(hào)線式賈忽悠的法拉第未來,有損法拉第的英明。此罪當(dāng)煮。
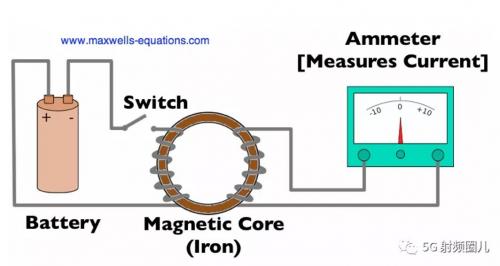
法拉第是一位科學(xué)家,早在19世紀(jì)30年代就開始試驗(yàn)電路和磁線圈。他的實(shí)驗(yàn)裝置導(dǎo)致了法拉第定律,如圖1所示:
實(shí)驗(yàn)本身有點(diǎn)簡(jiǎn)單。當(dāng)電池?cái)嚅_時(shí),我們沒有電流流過電線。因此,鐵(磁芯)內(nèi)沒有感應(yīng)磁通量。鐵就像一條通向磁場(chǎng)的高速公路——它們很容易流過磁性物質(zhì)。所以磁芯的作用是為磁通量創(chuàng)造一條路徑。
當(dāng)開關(guān)閉合時(shí),電流將在連接到蓄電池的導(dǎo)線內(nèi)流動(dòng)。當(dāng)電流流動(dòng)時(shí),它有一個(gè)相關(guān)的磁場(chǎng)(或磁通量)。當(dāng)導(dǎo)線纏繞在磁芯的左側(cè)(如圖1所示)時(shí),磁芯內(nèi)會(huì)產(chǎn)生磁場(chǎng)(磁通量)。這種磁通量繞著磁芯移動(dòng)。所以左邊的接線線圈產(chǎn)生的磁通量存在于右邊的接線線圈中,它與電流表相連。
現(xiàn)在,一件有趣的事情發(fā)生了,法拉第觀察到了。當(dāng)他關(guān)閉開關(guān)時(shí),電流會(huì)開始流動(dòng),電流表會(huì)單向尖峰(比如測(cè)量另一側(cè)的+10安培)。但這是非常短暫的,右邊線圈上的電流將歸零。當(dāng)開關(guān)斷開時(shí),測(cè)量的電流會(huì)向另一側(cè)尖峰(比如說,將測(cè)量-10安培),然后右側(cè)的測(cè)量電流將再次為零。
法拉第知道發(fā)生了什么。當(dāng)開關(guān)最初從開到關(guān)時(shí),磁芯內(nèi)的磁通量從零增加到某個(gè)最大值(這是一個(gè)恒定值,隨時(shí)間變化)。當(dāng)磁通量增加時(shí),在磁通的另一側(cè)存在感應(yīng)電流。
同樣,當(dāng)開關(guān)打開時(shí),磁芯中的磁通量也會(huì)從它的恒定值減小到零。因此,磁芯內(nèi)的磁通量減少會(huì)在右側(cè)產(chǎn)生相反的電流。
法拉第發(fā)現(xiàn),電路(或?qū)Ь€的閉環(huán))內(nèi)的磁通量變化會(huì)產(chǎn)生感應(yīng)電動(dòng)勢(shì)或電路內(nèi)的電壓。他這樣寫道:
在方程[2]中,磁通量是電路內(nèi)的磁通量,而電動(dòng)勢(shì)是電動(dòng)力,基本上是電壓源。方程[2]表明電路中的感應(yīng)電壓與磁通量的時(shí)間變化率相反。有關(guān)衍生工具的詳細(xì)信息,請(qǐng)參閱“部分衍生工具”頁。
方程[2]被稱為Lenz定律。倫茲是找出負(fù)號(hào)的人。我們知道電流會(huì)產(chǎn)生磁場(chǎng),但多虧了法拉第,我們也知道回路中的磁場(chǎng)會(huì)產(chǎn)生電流。宇宙喜歡對(duì)稱性,麥克斯韋方程有很多對(duì)稱性。
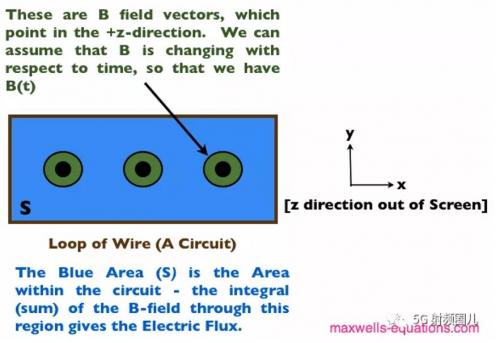
現(xiàn)在,我們得到了方程[2]的實(shí)驗(yàn)結(jié)果,我們?nèi)绾螐倪@個(gè)結(jié)果到方程[1]中法迪定律的標(biāo)準(zhǔn)形式?很高興你問我。讓我們想象一個(gè)簡(jiǎn)單的循環(huán),其中有一個(gè)時(shí)變的B字段:
我們知道,總磁通量的變化率等于電動(dòng)勢(shì)的反方向,即導(dǎo)線內(nèi)的電力。總磁通量只是導(dǎo)線所包圍區(qū)域上B場(chǎng)的積分(或和):
為了求出整個(gè)電路周圍感應(yīng)的總電動(dòng)勢(shì),我們把每一點(diǎn)產(chǎn)生的電動(dòng)勢(shì)加在電線的長度上。這就是所謂的線積分。本文寫成:
現(xiàn)在,回想一下,電場(chǎng)與電荷產(chǎn)生的力直接相關(guān)。電壓也被定義為路徑上電場(chǎng)的總和(積分)[回想一下,電場(chǎng)是以伏特/米為單位測(cè)量的]。因此,電場(chǎng)實(shí)際上是電壓的空間導(dǎo)數(shù)(電場(chǎng)等于電壓相對(duì)于距離的變化率)。這些事實(shí)總結(jié)如下:
因此,方程[4]和[5]告訴我們,沿著電路的任何點(diǎn)(在[4]中為dEMF)的EMF微分量等于該位置的E場(chǎng)。因此:
現(xiàn)在,一些數(shù)學(xué)家Stokes發(fā)現(xiàn),在一個(gè)環(huán)上積分(平均)一個(gè)場(chǎng)就等于在環(huán)內(nèi)積分這個(gè)場(chǎng)的旋度。這對(duì)你來說應(yīng)該有一個(gè)直觀的事實(shí):旋度是場(chǎng)旋轉(zhuǎn)的量度,因此曲面內(nèi)向量場(chǎng)的旋度應(yīng)該與圍繞曲面的環(huán)的場(chǎng)的積分有關(guān)。如果沒有意義,請(qǐng)多想想,或者接受以下事實(shí)(因?yàn)樗钦娴摹粌H是E字段,而且是任何字段):
現(xiàn)在我們就快到了。如果我們用方程[3]和方程[7]中的項(xiàng)替換方程[2]的Farday定律,那么我們得到:
在方程[8]中,我們注意到如果我們?cè)谇嫔嫌袃蓚€(gè)積分,并且曲面可以是我們選擇的,那么我們積分的量也必須是相同的。這就是我們?nèi)绾蔚玫椒ɡ诙傻淖罱K形式,如麥克斯韋方程所列!
法拉第定律表明,回路中磁場(chǎng)的變化會(huì)產(chǎn)生感應(yīng)電流,感應(yīng)電流是由回路中的力或電壓引起的。我們可以這樣說法拉第定律:
電流產(chǎn)生磁場(chǎng)。電路周圍的磁場(chǎng)產(chǎn)生電流。
磁場(chǎng)隨著時(shí)間的變化會(huì)產(chǎn)生一個(gè)圍繞它循環(huán)的電場(chǎng)。
隨著時(shí)間的推移,一個(gè)循環(huán)的電場(chǎng)會(huì)產(chǎn)生一個(gè)隨時(shí)間變化的磁場(chǎng)。
法迪定律是非常強(qiáng)大的,因?yàn)樗@示了宇宙是多么熱愛對(duì)稱。如果電流產(chǎn)生磁場(chǎng),磁場(chǎng)就會(huì)產(chǎn)生電流。空間中的E場(chǎng)的變化會(huì)導(dǎo)致時(shí)間上的B場(chǎng)的變化。當(dāng)我們繼續(xù)看麥克斯韋方程的最后一個(gè),安培定律,我們會(huì)看到更多的對(duì)稱性!
式4 安培定律
安培是一位科學(xué)家,他在試驗(yàn)載電流的電線上的力。早在19世紀(jì)20年代,他就在做這些實(shí)驗(yàn),幾乎和法迪研究法拉第定律的時(shí)間一樣。安培和法迪不知道,大約40年后,麥克斯韋自己會(huì)把工作統(tǒng)一起來。
電線上的力量對(duì)我來說不是特別有趣,因?yàn)樵谖业墓ぷ鬟^程中,我從來沒有機(jī)會(huì)使用非常復(fù)雜的方程式(包括博士學(xué)位,在國家實(shí)驗(yàn)室的一些工作,以及國防和消費(fèi)電子行業(yè)的就業(yè))。所以,我將首先介紹安培定律,它涉及電流和圍繞它的磁場(chǎng):
方程[2]可以解釋為:假設(shè)有一個(gè)導(dǎo)體(導(dǎo)線)攜帶電流,那么這個(gè)電流產(chǎn)生一個(gè)繞導(dǎo)線旋轉(zhuǎn)的磁場(chǎng)。
方程[2]的左邊是指:如果你沿著環(huán)繞導(dǎo)線的任何一條假想路徑,把沿著該路徑的每一點(diǎn)的磁場(chǎng)相加,那么它將在數(shù)值上等于被該路徑環(huán)繞的電流量(這就是為什么我們把環(huán)繞電流寫為環(huán)繞電流或環(huán)繞電流的原因)。
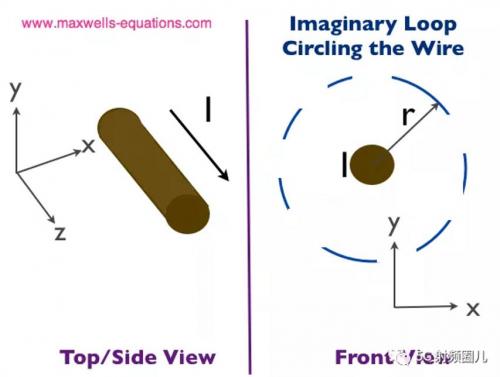
讓我們做一個(gè)有趣的例子。假設(shè)我們有一根長電線,它承載著恒定的電流,I[安培]。距離導(dǎo)線任意距離r[米]時(shí),導(dǎo)線周圍的磁場(chǎng)是多少?
讓我們看看圖1中的圖表。我們有一根載電流為安培的長電線。我們想知道在距離導(dǎo)線r的地方磁場(chǎng)是多少。所以我們?cè)陔娋€周圍畫了一條假想的路徑,這是圖1右邊的藍(lán)色虛線:
安培定律[方程式2]指出,如果我們沿著這條藍(lán)色路徑把磁場(chǎng)加起來(積分),那么在數(shù)值上這應(yīng)該等于封閉電流I。
現(xiàn)在,由于對(duì)稱性,磁場(chǎng)在距離導(dǎo)線r處是均勻的(不是變化的)。圖1中藍(lán)色路徑的路徑長度等于半徑r的圓的周長。
如果我們把磁場(chǎng)的一個(gè)常數(shù)相加(我們稱之為H),那么方程[2]的左邊就變得簡(jiǎn)單了:
因此,我們已經(jīng)知道了H場(chǎng)的大小。既然r是任意的,我們知道H場(chǎng)在哪里。方程[3]指出,當(dāng)你遠(yuǎn)離導(dǎo)線時(shí)(由于1/r項(xiàng)),磁場(chǎng)的大小會(huì)減小。
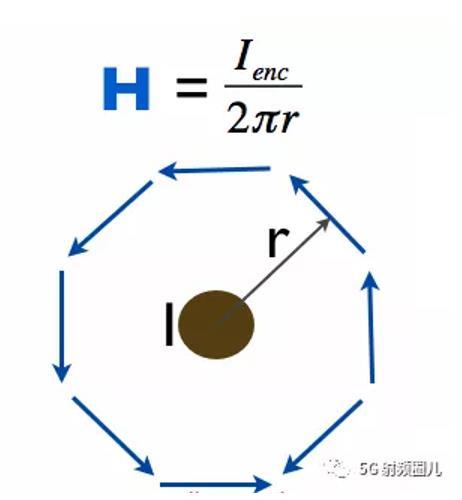
所以我們用安培定律(方程式[2])來計(jì)算繞著電線的磁場(chǎng)的大小。然而,H場(chǎng)是向量場(chǎng),這意味著在每個(gè)位置is都有一個(gè)量值和一個(gè)方向。H場(chǎng)的方向與虛環(huán)相切,如圖2所示。右手法則決定磁場(chǎng)的方向:
我們要用斯托克定理做同樣的技巧,就像我們?cè)诳捶ɡ诙蓵r(shí)做的一樣。我們可以重寫方程式[2]中的安培定律:
在方程[4]的右邊等式中,我們利用Stokes定理將一個(gè)閉合環(huán)周圍的線積分,通過環(huán)所包圍的曲面,轉(zhuǎn)化為同一場(chǎng)的旋度。
我們還可以將總電流(I)重寫為電流密度(J)的表面積分:
現(xiàn)在我們用表面積分(方程[4]和[5])重寫了原來的安培定律(方程[2])。因此,我們可以把它們放在一起,得到安培定律的一種新形式:
現(xiàn)在,我們有了一種新的安培定律:磁場(chǎng)的旋度等于電流密度。如果你是一個(gè)聰明的學(xué)習(xí)者,你可能會(huì)注意到方程式[6]不是最后的形式,它是寫在方程式[1]中的。方程[6]有一個(gè)問題,但直到19世紀(jì)60年代,詹姆斯·克拉克·麥克斯韋才發(fā)現(xiàn)這個(gè)問題,并把電磁學(xué)與麥克斯韋方程統(tǒng)一起來。
至此,麥克斯韋方程全部講完,不知道小伙伴們對(duì)麥克斯韋方程組有沒有加深印象。沒有的話,繼續(xù)往下看:
四,簡(jiǎn)明扼要說Maxwell Equation
到目前為止,我已經(jīng)單獨(dú)討論了麥克斯韋方程。在這一頁上,我想再次給出他們的概述-沒有數(shù)學(xué)-并解釋他們作為一個(gè)整體的含義。
4.1高斯定律
高斯定律等價(jià)于電荷的力方程:相似電荷相互排斥,相反電荷(正電荷和負(fù)電荷)相互吸引。
高斯定律還說電場(chǎng)線偏離電荷。這意味著正電荷是電場(chǎng)的來源(就像水龍頭是水源一樣)。高斯定律是指負(fù)電荷作為電場(chǎng)的水槽(水通過水槽孔排出或離開一個(gè)區(qū)域的方式)。這意味著電場(chǎng)線在充電時(shí)開始和停止。
4.2磁學(xué)高斯定律
麥克斯韋的第二個(gè)方程表示磁單極子不存在。當(dāng)我們有電荷(電單極子)時(shí),我們從未發(fā)現(xiàn)磁等價(jià)物——磁電荷或磁單極子。這個(gè)方程表明磁場(chǎng)傾向于環(huán)繞物體,因?yàn)樯⒍葹榱悖艌?chǎng)傾向于形成閉合環(huán)。
4.3法拉第定律
法拉第定律告訴我們,隨著時(shí)間變化的磁場(chǎng)會(huì)產(chǎn)生一個(gè)循環(huán)的電子場(chǎng)。這意味著我們有兩種產(chǎn)生電場(chǎng)的方法——從電荷(或流動(dòng)電荷、電流)或從正在變化的磁場(chǎng)。
4.4安培定律
安培定律告訴我們,流動(dòng)的電流產(chǎn)生一個(gè)繞著電線的磁場(chǎng)。除此之外,它還說隨著時(shí)間變化的電場(chǎng)會(huì)產(chǎn)生一個(gè)圍繞著電場(chǎng)的磁場(chǎng)——這是麥克斯韋自己提出的位移電流項(xiàng)。
這意味著有兩種方法可以產(chǎn)生一個(gè)螺線管(循環(huán))H-場(chǎng)-一個(gè)流動(dòng)的電流或一個(gè)變化的電場(chǎng)。兩者都會(huì)產(chǎn)生同樣的現(xiàn)象。
總的來說,麥克斯韋方程是什么意思?
前兩種主要用于直流電,即當(dāng)所有電壓和電流都是恒定的,且沒有隨時(shí)間變化的情況下。這些在我看來不太重要,事實(shí)上,它們可以從第二組方程中導(dǎo)出。因此,這是后兩個(gè)版本的一個(gè)較弱的版本。
第三和第四個(gè)方程確實(shí)規(guī)定了電場(chǎng)和磁場(chǎng)的規(guī)則。例如,在一種被稱為時(shí)域有限差分法(FDTD)的電磁學(xué)解算器中,只有后兩個(gè)方程用于E場(chǎng)和H場(chǎng)的數(shù)值求解。前兩個(gè)不需要。
讓我們來看看第三和第四個(gè)方程,這兩個(gè)簡(jiǎn)潔的陳述支配了所有的E場(chǎng)和H場(chǎng)傳播:
法拉第定律說,變化的磁場(chǎng)產(chǎn)生一個(gè)旋轉(zhuǎn)的電場(chǎng)。現(xiàn)在,宇宙中的事物不會(huì)持續(xù)增長或持續(xù)收縮——它們會(huì)振蕩(以平均值上下移動(dòng))。這意味著磁場(chǎng)先增大后減小,這意味著電場(chǎng)在一個(gè)不斷變化的磁場(chǎng)周圍來回纏繞。這意味著電場(chǎng)也在隨時(shí)間變化。
現(xiàn)在看看安培定律。這意味著一個(gè)變化的電場(chǎng)會(huì)產(chǎn)生一個(gè)旋轉(zhuǎn)的磁場(chǎng)。同樣地,電場(chǎng)也會(huì)在時(shí)間上振蕩,環(huán)繞磁場(chǎng)也會(huì)在時(shí)間上變化。
讓我們想想最后兩段。不斷變化的磁場(chǎng)產(chǎn)生不斷變化的電場(chǎng)。而不斷變化的電場(chǎng)會(huì)產(chǎn)生不斷變化的磁場(chǎng)——磁場(chǎng)本身會(huì)產(chǎn)生不斷變化的電場(chǎng),從而產(chǎn)生。。。。。
這是什么?這種現(xiàn)象稱為傳播。這就是電磁波傳播的原因。這是一個(gè)永恒的運(yùn)動(dòng)輪,它使太陽光在真空中傳播,而不需要任何介質(zhì)。從這兩個(gè)方程中我們可以確定所有傳播的波都以單一的速度傳播,即光速。這個(gè)速度可以直接由麥克斯韋方程中的常數(shù)決定。
每一種電磁形式或輻射——可見光、x射線、加熱地球的太陽光、無線電波、電視波、wifi信號(hào)、藍(lán)牙信號(hào)、手機(jī)傳輸和GPS——都完全由電場(chǎng)和磁場(chǎng)組成。你所需要知道的關(guān)于它們?nèi)绾蝹鞑ズ团c物質(zhì)相互作用的一切,都完全由上述兩個(gè)方程決定,這兩個(gè)方程在19世紀(jì)60年代由詹姆斯·克拉克·麥克斯韋統(tǒng)一解釋。
讓我們記住這個(gè)人詹姆斯·克拉克·麥克斯韋


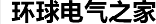

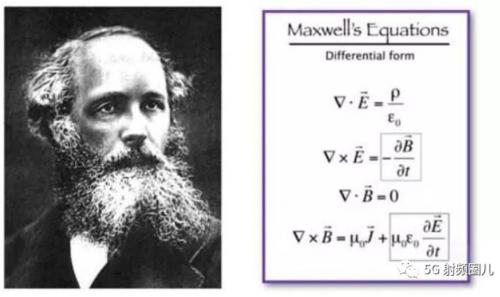


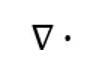
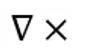


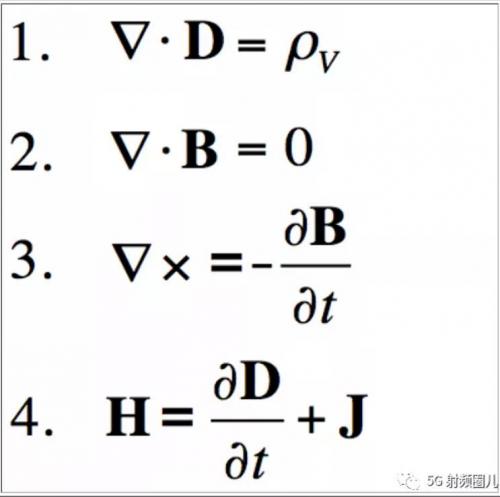

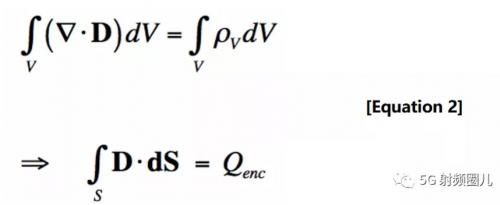


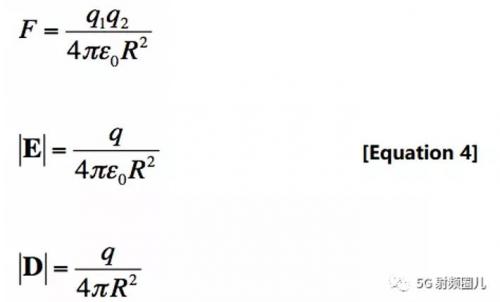









![方程[3]和方程[7]中的項(xiàng)替換方程[2]的Farday定律](https://upload.semidata.info/sns.eefocus.com/rf/article/media/2021/11/23/355386.jpg)
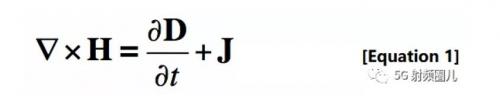

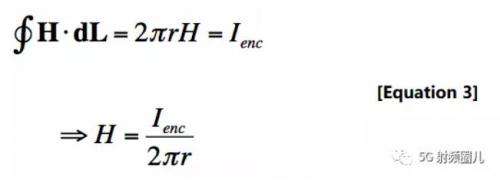
![重寫方程式[2]中的安培定律](https://upload.semidata.info/sns.eefocus.com/rf/article/media/2021/11/23/355405.jpg)

![表面積分(方程[4]和[5])重寫了原來的安培定律(方程[2]](https://upload.semidata.info/sns.eefocus.com/rf/article/media/2021/11/23/355373.jpg)
